In the previous post I described how I learned about HEALPix because I wanted to try covering a sphere with square tiles for a game map. During that exploration I realized that HEALPix with 12 square regions is similar to cubes with 6 square regions, but HEALPix has some nice properties for numerical calculations such as spherical harmonics. I don't need those properties. Instead, I am looking for something that's simpler to program, so I explored cubes.

The goal is the same: I want to play a game on a flat top-down tile map (roguelikes, Dwarf Fortress, Factorio, etc.), but these games have one of three approaches to the map:
- The map is finite and has borders. You can't move past the border. Most roguelikes fall into this category. SimCity, Dwarf Fortress, and most building games do as well.
- The map is finite and but some borders allow wrapping. Civilization allows east/west wrapping (cylinder); Asteroid has both east/west and allow north/south wrapping (torus).
- The map is infinite, so it has no borders. Factorio works this way, with a procedurally generated map.
I wanted to explore type 2, but with a sphere instead of a cylinder or torus. The usual approaches to representing a sphere with flat tiles is to use one of the 5 Platonic solids: tetrahedron, cube, octahedron, dodecahedron, isocahedron. There are also approaches that aren't based on Platonic solids: HEALPix, Mercator-like projections, Peirce Quincucial, and others.
In the previous post I mentioned that this is a "gamejam" style project. I give myself one week to work on the topic, and then I wrap it up. If I found something interesting I'll write it up, but many times I'll discard the project. Allowing myself to discard projects removes the penalty for making a "wrong turn". This allows me to explore more quickly.
After HEALPix I decided to explore cubes for the next week's project, using cube maps from graphics programming. It turned out not to be so useful. I had made a wrong turn. That's ok! Because each of these is a separate standalone tiny project, I can easily abandon the code and move on.
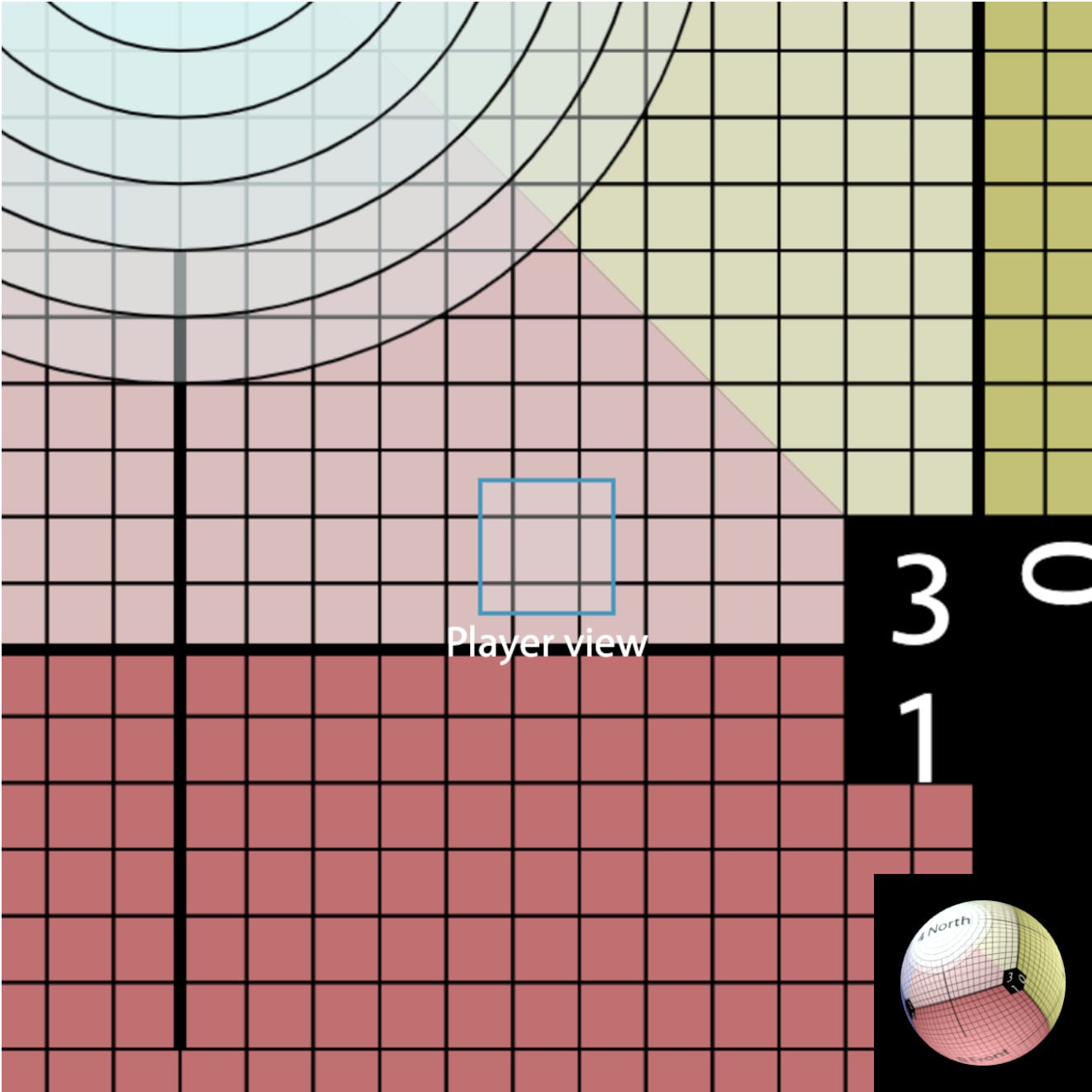
The week after that worked pretty well. I was able to learn how to render and also represent a square grid map on a sphere/cube.
I wrote notes about square tiles on a cube/sphere, including some animations showing how a cube morphs into a sphere, how a cube unfolds onto a plane, and how there are different ways to project a grid on the sphere.
The next "gamejam" style project will be to generate a map on this sphere.
No comments:
Post a Comment